Variational Quantum Classifier Using Cirq with Optimized Encoding Parameters
This series of code snippets demonstrates the implementation of a quantum machine learning model using Cirq, a Python SDK from Google for quantum computing
Our focus here is to dive into a simple implementation of a quantum machine learning model using Cirq (Google's quantum computing library).
Before we embark on this journey, let's set the stage by understanding the tools we'll be using. At the heart of our exploration is Cirq, an open-source framework developed by Google for building and experimenting with quantum algorithms on simulated quantum computers. To complement this, we integrate tools from the well-established SciPy library, particularly its minimize function, for optimizing our quantum model.
In this post, we'll walk through a quantum machine learning model step-by-step, from encoding data and constructing variational circuits to optimizing the model and making predictions. Whether you're a seasoned quantum enthusiast or a curious newcomer to the field, this exploration is designed to provide valuable insights into how quantum computing can augment machine learning capabilities.
Remember to Follow the Pre-process Step
Below you can find another post about how you should prepare your dataset to continue with the code exposed in this article.
Dimensionality Reduction for Quantum Machine Learning: Integrating LDA and K-Means
In Quantum Machine Learning (QML), the preparation of data is a crucial step that often determines the effectiveness and efficiency of the algorithms used. One of the key challenges in this process is dimensionality reduction, which involves transforming high-dimensional data into a lower-dimensional space. This is particularly important in quantum comp…
Data Encoding into Quantum States
def encode_data(qubits, data_point, parameters):
circuit = cirq.Circuit()
for i, feature in enumerate(data_point):
circuit.append(cirq.ry(feature * parameters[i])(qubits[i]))
return circuitPurpose: This function encodes classical data points into quantum states.
How It Works:
It iterates over each feature in the
data_point.For each feature, it applies a rotation around the Y-axis (
cirq.ry) on the corresponding qubit. The angle of rotation is determined by the product of the feature value and a parameter (feature * parameters[i]).
Parameters:
qubits: The list of qubits in the quantum circuit.data_point: A single instance of the dataset (a vector of features).parameters: The set of parameters used for the rotation gates.
This particular data encoding allows for little adaptations of the input data through those parameters that have been added. Allows for better encoding in the presence of noise and emphasizing or boosting features that might have a higher correlation with the target we would like to predict. One should pay attention to the outcome though, as in some cases, depending on the sample balance it could turn those features into a set of zeros eliminating the contribution of the data to the whole process. This is quite common in unbalanced datasets so we will keep that in mind during training as one of the metrics to monitor as well.
Variational Quantum Circuit
def variational_circuit(qubits, parameters):
circuit = cirq.Circuit()
for i, qubit in enumerate(qubits):
circuit.append(cirq.rx(parameters[i+len(qubits)])(qubit))
for i in range(len(qubits) - 1):
circuit.append(cirq.CNOT(qubits[i], qubits[i+1]))
for i, qubit in enumerate(qubits):
circuit.append(cirq.measure(qubit, key=f'm{i}'))
return circuitPurpose: Constructs the variational part of the quantum circuit.
How It Works:
It applies parameterized rotations along the X-axis (
cirq.rx) on each qubit. These rotations are controlled by the second half of theparametersarray.It then creates entanglement between adjacent qubits using CNOT gates. Entanglement is a key feature of quantum circuits, allowing for complex correlations.
Finally, it measures each qubit, assigning a unique key for each measurement. These measurements are used to extract classical information from the quantum state.
Cost Function for Model Optimization
def cost_function(params, X, Y, qubits, lambda_reg=0.001):
loss = 0.0
for x, y in zip(X, Y):
circuit = cirq.Circuit()
circuit += encode_data(qubits, x, params)
circuit += variational_circuit(qubits, params)
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=100)
total_p0 = 0
for i in range(len(qubits)):
counts = result.histogram(key=f'm{i}')
p0 = counts.get(0, 0) / 100
total_p0 += p0
loss += (total_p0/len(qubits) - y) ** 2
reg_term = lambda_reg * np.sum(params**2)
return loss + reg_termPurpose: Defines the cost function to evaluate the model's performance.
How It Works:
The function iterates over each pair of data point (
x) and its label (y).For each pair, it creates a quantum circuit combining the encoding and variational circuits.
The circuit is executed using a simulator, and the measurement results are used to calculate the probability of each qubit being in the
|0⟩state.The loss is calculated as the mean squared error between these probabilities and the actual labels (
y).A regularization term (
reg_term) is added to the loss to prevent overfitting by penalizing large values of the parameters.
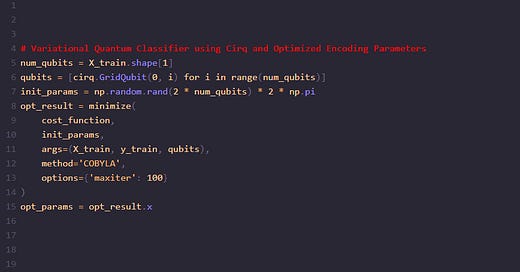
Training the Quantum Model
num_qubits = X_train.shape[1]
qubits = [cirq.GridQubit(0, i) for i in range(num_qubits)]
init_params = np.random.rand(2 * num_qubits) * 2 * np.pi
opt_result = minimize(
cost_function,
init_params,
args=(X_train, y_train, qubits),
method='COBYLA',
options={'maxiter': 100}
)
opt_params = opt_result.xPurpose: Initializes the quantum circuit and finds the optimal parameters for the model.
How It Works:
Determines the number of qubits needed based on the number of features in
X_train.Initializes the qubits and sets up random initial parameters for the rotations in the circuit.
Uses a classical optimization algorithm (COBYLA) to minimize the cost function. The
minimizefunction iteratively adjusts the parameters and evaluates the cost function to find the set of parameters that yields the lowest loss.
Making Predictions with the Trained Model
def predict(X, params, qubits, threshold=0.5):
predictions = []
for x in X:
circuit = cirq.Circuit()
circuit += encode_data(qubits, x, params)
circuit += variational_circuit(qubits, params)
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=100)
total_p0 = 0
for i in range(len(qubits)):
counts = result.histogram(key=f'm{i}')
p0 = counts.get(0, 0) / 100
total_p0 += p0
avg_p0 = total_p0 / len(qubits)
predictions.append(1 if avg_p0 > threshold else 0)
return predictionsPurpose: To use the trained quantum circuit for making predictions on new data.
How It Works:
For each data point in
X, it constructs and runs the quantum circuit (comprising data encoding and variational parts).Measures the probability of each qubit being in the
|0⟩state.Calculates the average of these probabilities and compares it to a threshold to make a binary prediction.
Using the Prediction Function
predictions = predict(X_test, opt_params, qubits)Process: This line of code applies the predict function on the test dataset X_test using the optimized parameters opt_params.
Evaluating the Model's Performance
accuracy = np.mean(np.array(predictions) == y_test)
print(f"Predictions: {predictions}")
print(f"Test accuracy: {accuracy * 100:.2f}%")Function: predict_proba
def predict_proba(X, params, qubits):
probabilities = []
for x in X:
circuit = cirq.Circuit()
circuit += encode_data(qubits, x, params)
circuit += variational_circuit(qubits, params)
simulator = cirq.Simulator()
result = simulator.run(circuit, repetitions=100)
total_p0 = 0
for i in range(len(qubits)):
counts = result.histogram(key=f'm{i}')
p0 = counts.get(0, 0) / 100
total_p0 += p0
avg_p0 = total_p0 / len(qubits)
probabilities.append(avg_p0)
return probabilitiesPurpose: To compute the predicted probabilities for each data point in
Xusing the quantum circuit.How It Works:
Iterates over each data point in
X.Constructs a quantum circuit that includes both data encoding and the variational circuit, using the provided parameters.
Runs the circuit on a simulator for a fixed number of repetitions, gathering measurement results.
For each qubit, calculates the probability of observing the state
|0⟩(denoted asp0).Averages these probabilities across all qubits to determine the overall probability for each data point.
Appends this average probability to a list, which represents the predicted probability distribution of the dataset.
Extracting an AUC
probabilities = predict_proba(X_test, opt_params, qubits)
fpr, tpr, thresholds = roc_curve(y_test, probabilities)
roc_auc = auc(fpr, tpr)
print(f"AUC: {roc_auc}")Purpose: To evaluate the performance of the quantum machine learning model.
How It Works:
Uses the
predict_probafunction to compute the predicted probabilities for the test datasetX_test.roc_curvefunction from the scikit-learn library is used to compute the Receiver Operating Characteristic (ROC) curve, which is a graphical representation of the model's diagnostic ability.The
aucfunction calculates the Area Under the ROC Curve (AUC), a measure of the model's overall performance. A higher AUC indicates a better model.Finally, the AUC value is printed, providing a concise and informative summary of the model's predictive accuracy.