Quantum Feature Selection Made Easy

How to use Falcondale OSS for an easy quantum feature selection process.

We will go deep on how feature selection can be tackled using current quantum computing means. We will see how it is formulated with coded examples and how it can be transferred to quantum and quantum-inspired solvers to obtain our best subset.

Finally, a simple version was made available in Falcondale OSS, which may be the best option in terms of complexity. Let’s get started.

Feature Selection

Many times, when a dataset is handed over to us, we might need to check if all features contribute to the goal at hand. It might be that some of them add no information or overlap between them, making it more time-consuming to train a model out of an initial set of data. Other approaches can also be used, like Principal Component Analysis (PCA) but they tend to obscure the actual information used for inference. Feature selection offers a way to select a subset that maximizes the amount of information contained for the task while reducing the initial set of attributes.

Let’s check a canonical case, Scikit-Learn’s Breast Cancer dataset:

pip install sklearn

Then, we can import the dataset from our code:

from sklearn.datasets import load_breast_cancer

dataset = load_breast_cancer(as_frame=True)
df = dataset['data']
df['target'] = dataset['target']
df

See, we have a set of features and a target variable (named target), and we should decide which features contribute to predicting it.

A common way to do this is by simply training, for example, a tree-based model and extracting the feature importance. A more intensive search is the one performed by Recursive Feature Elimination (RFE) that trains models on subsets looking for those features that have no effect on model performance. But these techniques are quite demanding, depending on the model we choose, and may leave some good subsets out just out of chance.

Quantum Feature Selection

Quantum Feature Selection (QFS) simply poses the above problem as a QUBO/Ising type of problem and tries to find the selection of features that minimizes its energy. Let’s proceed step by step.

A feature is as important as its information capacity with respect to the target variable. We could characterize this by its mutual information I(X;Y) which is nothing other than the overlap between the information of our target variable Y and a particular feature X. Essentially, it quantifies how much we can understand one variable by looking at the other.

Scikit-Learn offers a simplistic way to compute this by simply calling:

from sklearn.feature_selection import mutual_info_classif

X = dataset['data'].drop(columns=["target"])
y = dataset['target']

mi = mutual_info_classif(X, y)

This way mi holds the mutual information for each of our variables and the target variable Y.

Now, removing those that have little overlap may be a good option, but it is more interesting if we can also remove those that offer redundant information.

For this, we would need to compute the overlap between X and Y given the variable Z (a third feature within our feature set). This way, we can assess how much information is overlapped between X and Z and decide to remove one of them, ideally the one that has a lower I(X;Y).

Conditional Mutual Information is described as

\(I(X;Y|Z) = I(X;Y,Z) - I(X;Z)\)

and can be computed as follows:

import pandas as pd
import numpy as np

def conditional_mutual_information(data, X, Y, Z, delta = 1):
    cmi = 0

    P_Z = data.groupby(Z).size()
    P_Z = P_Z/P_Z.sum()

    P_XZ = data.groupby(X + Z).size()
    P_XZ = P_XZ/P_XZ.sum()

    P_YZ = data.groupby(Y + Z).size()
    P_YZ = P_YZ/P_YZ.sum()

    P_XYZ = data.groupby(X + Y + Z).size()
    P_XYZ = P_XYZ/P_XYZ.sum()

    for ind in P_XYZ.index:
        x_ind = ind[:len(X)]
        y_ind = ind[len(X):len(X + Y)]
        z_ind = ind[len(X + Y):]

        xz_ind = x_ind + z_ind
        yz_ind = y_ind + z_ind
        xyz_ind = ind

        z_ind =  pd.MultiIndex.from_tuples([z_ind], names = Z) if len(Z) != 1 else pd.Index(z_ind, name = Z[0])
        xz_ind = pd.MultiIndex.from_tuples([xz_ind], names = X + Z)
        yz_ind = pd.MultiIndex.from_tuples([yz_ind], names = Y + Z)
        xyz_ind = pd.MultiIndex.from_tuples([xyz_ind], names = X + Y + Z)

        cmi += delta * P_XYZ[xyz_ind].item() * np.log2(P_Z[z_ind].item() * P_XYZ[xyz_ind].item() / (P_XZ[xz_ind].item() * P_YZ[yz_ind].item()))

    return cmi

With that, one can simply go over all the columns and compute their conditional mutual information.

conditional_mutual_information(df, ['mean radius'], ['target'], ['mean area'])

Now, how do we convert this into an Ising hamiltonian? Well, if we consider the mutual information as the contribution of each variable and the conditional mutual information as the redundancy coefficient between variable pairs, we could map the problem to an Ising type of problem where variables represent the mask selection over dataset features (0 not selected, 1 selected).

\(H = - \sum_i^N h_i s_i + \sum^N_i \sum^N_{j, i \ne j} J_{ij}s_is_j \)

Composing this Hamiltonian could be done already, considering the final destination. The PyQUBO library could help us with that. We would also need to select the number of variables we would like to limit our selection to and add it as a regularization term.

from pyqubo import Array, Placeholder, Constraint

def qfs_problem(input_ds:pd.DataFrame, target:str, max_feat:int = None):
    """
    Takes the input data and creates a pyqubo model so that Ising
    coefficients can be extracted.
    """

    col_list = input_ds.columns
    feat_list = [ col for col in col_list if col != target]
    num_assets = len(feat_list)
    x = Array.create('x', shape=num_assets, vartype='BINARY')

    # Feature importance computed as the mutual information
    H_importance = 0.0
    for i, column in enumerate(feat_list):
        if column != target:
            minf = mutual_info_classif(input_ds[[column]], input_ds[[target]])

            H_importance += Constraint(
                minf[0] * x[i], label='relevance({})'.format(i)
            )

    # Feature redundancy as conditioned mutual information
    H_redundancy = 0.0
    for i, field0 in enumerate(feat_list):
        for j, field1 in enumerate(feat_list):
            if field0 != field1:
                cmi_01 = conditional_mutual_information(
                    input_ds, [field0], [target], [field1])
                H_redundancy += Constraint(
                    cmi_01 * x[i] * x[j], label='redundancy({}, {})'.format(i, j)
                )

    # Constraint (budget)
    H_penalty = 0.0
    for i in range(num_assets):
        H_penalty += Constraint(x[i], label='selected({})'.format(i))

    # Build model (min direction)
    lamda = Placeholder('lambda')
    H =  H_redundancy - H_importance + lamda * (H_penalty - max_feat)**2

    return H.compile()

With this, you can simply call your model to be computed.

model = qfs_problem(df, "target", 1)

And call for the Ising coefficients.

model.to_ising(feed_dict = {"lambda" : 100})

D-Wave plugin

I know there is quite some code and work to do. That is why people from DWave considered building a plugin you can install that should simplify your life, as they already built the model for you, and you simply need to select the number of features and dataset to be used.

pip install dwave-scikit-learn-plugin

This makes our life much easier, as we only need to code:

from dwave.plugins.sklearn import SelectFromQuadraticModel

max_features = 6

model = SelectFromQuadraticModel(num_features=max_features)
model.fit(X, y)

And obtain the selected features by their name:

selected = model.get_feature_names_out(sub_selection)

But if we would like to test other methods to solve our Ising type of problem, we will definitely need to build the previous model and then the corresponding circuit for let’s say, QAOA or quantum-inspired methods like simulated bifurcation.

Check out more information about D-Wave’s FS here:

Falcondale OSS

This is why Falcondale exists. The aim is to ease this tests so that simple codes can be developed to test and benchmark different solutions.

First you will need to install it

pip install falcondale-sdk

Once installed, data needs to be provided starting a new Project

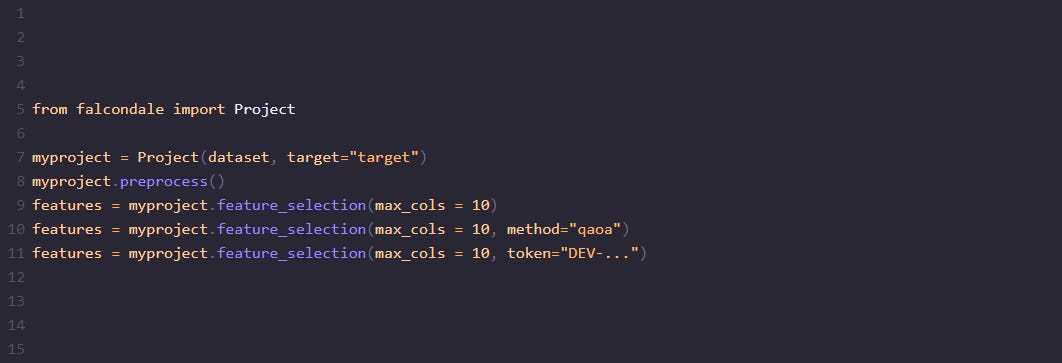
from falcondale import Project

myproject = Project(dataset, target="target")
myproject.preprocess()

By default, simulated annealing can be tested

features = myproject.feature_selection(max_cols = 10)

But it also allows for QAOA

features = myproject.feature_selection(max_cols = 10, method="qaoa")

Or simulated bifurcation implementation solutions.

features = myproject.feature_selection(max_cols = 10, method="sb")

It should also ease your life when using D-Wave as it comes integrated as well and when the token is provided it directly ships the process to D-Wave’s service.

features = myproject.feature_selection(max_cols = 10, token="DEV-...")

So it is up to you which method you should use. Simply use the method parameter and enjoy.